30-60-90 Triangle Formula

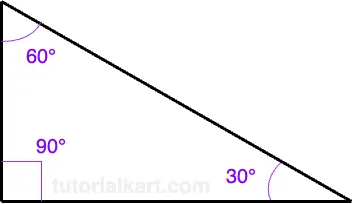
Introduction to 30-60-90 Triangle Formula

A 30-60-90 triangle is a special type of right triangle that has angle measures of 30°, 60°, and 90°.

What makes this triangle unique is that the sides of the triangle follow a consistent ratio, allowing us to easily calculate the lengths of any side if we know one of them.

In this tutorial, we’ll cover the characteristics of a 30-60-90 triangle, the formula to calculate the sides, and how to apply it in various examples.

Properties of a 30-60-90 Triangle

In a 30-60-90 triangle:

• The 90° angle is the right angle.
• The 30° angle is the smallest angle.
• The 60° angle is the second largest angle.
• The sides of the triangle follow a specific ratio based on these angles.

Side Length Ratios

The sides of a 30-60-90 triangle are always in the ratio:

$$1:\sqrt{3}:2$$

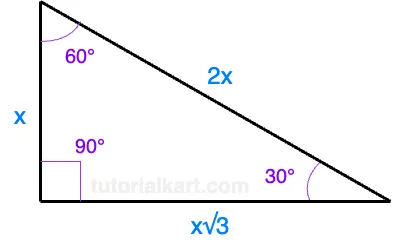
Here’s how the ratio corresponds to the sides of the triangle:

• The shortest side (opposite the 30° angle) is $x$, which is height in the above diagram.
• The longer leg (opposite the 60° angle) is $x\sqrt{3}$, which is base in the above diagram.
• The hypotenuse (opposite the 90° angle) is $2x$.

Knowing this ratio, you can determine the length of any side of the triangle as long as you know one of the sides.

Formula for the 30-60-90 Triangle

If you know one side of a 30-60-90 triangle, you can use the following formulas to find the other sides:

If you know the shorter leg (opposite the 30° angle):

$$\text{Longer leg}=x\sqrt{3}$$

$$\text{Hypotenuse}=2x$$

If you know the longer leg (opposite the 60° angle):

$$\text{Shorter leg}=\frac{\text{Longer leg}}{\sqrt{3}}$$

$$\text{Hypotenuse}=2\times \left(\frac{\text{Longer leg}}{\sqrt{3}}\right)$$

If you know the hypotenuse:

$$\text{Shorter leg}=\frac{\text{Hypotenuse}}{2}$$

$$\text{Longer leg}=\frac{\text{Hypotenuse}}{2}\times \sqrt{3}$$

Example Calculations

Let’s look at some example calculations to understand how these formulas work.

Example 1: Finding the longer leg and hypotenuse

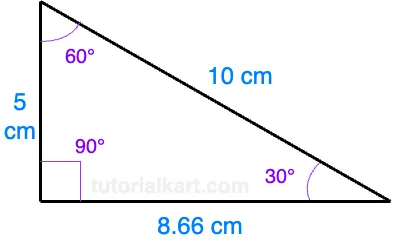
Given a 30-60-90 triangle where the shorter leg (opposite the 30° angle) is 5 cm, we can calculate the lengths of the other sides:

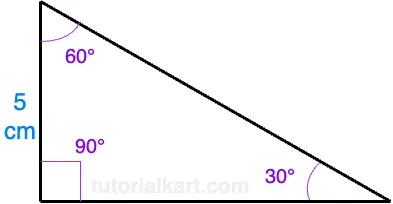
Using the formula for the longer leg:

$$\text{Longer leg}=5\times \sqrt{3}\approx 5\times 1.732=8.66\text{cm}$$

Using the formula for the hypotenuse:

$$\text{Hypotenuse}=2\times 5=10\text{cm}$$

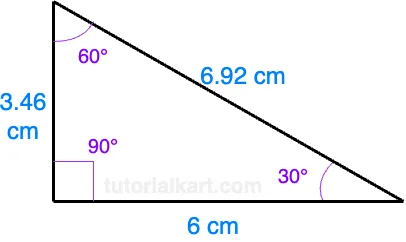
Example 2: Finding the shorter leg and hypotenuse

If the longer leg (opposite the 60° angle) is 6 cm, we can find the shorter leg and the hypotenuse:

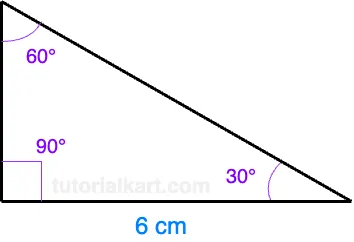
Using the formula for the shorter leg:

$$\text{Shorter leg}=\frac{6}{\sqrt{3}}\approx \frac{6}{1.732}=3.46\text{cm}$$

Using the formula for the hypotenuse:

$$\text{Hypotenuse}=2\times 3.46=6.92\text{cm}$$